1. Simulation of a cooling cup of coffee
We found that when we varied parameters Rth and C:
Higher Rth and C= smaller dT and thterefore the less the temperature will change
Lower Rth and C =larger dT and therefore the more the temperature will change
 |
| Original Coffee Plot R=.85 C=10,000 |
 |
| Coffee Plot Rth=10 |
 |
| Coffee Plot Rth=.15 |
 |
| Coffee Plot C=50 |
 |
| Coffee Plot C=1,000,000 |
We found that if we want our coffee to heat up to the Starbucks ideal 84 degrees C
This was calculated by using the equation (shown below) and isolation the value P with
T=375 because that's what we want the coffee temperature to be (the heater temperature)
We then incorporated the heater into the program to see hoe the heater effected the program and we could deduce that:
Rth is the change in final temperature divided by P, which means that final temperature difference depends only on P and Rth. And at equilibrium energy into the system is balanced by energy out.
C is equal to P times dT/dt so at t=0 the slope of the graph is equal to P/C
3. Feedback and Control: Bang Bang
Bang Bang control is appropriate for many thermal systems because it either turns on or off which is good because we only need it to do one thing set the temperature in the room equal to the value inputted, but it is insufficient because if the temperature goes over the right temperature it will have to keep turning itself on and off to again reach the goal temperature.
 |
| A zoomed in picture of the plot |
4. Proportional Control
Compared to Bang Bang, Proportional control takes a far longer time to reach the desired temperature, this is due to the very nature of proportional control which "slows down" once it gets close to the goal. These models makes sense because in real life thermometers use bang bang control instead of proportional control, and when we compare the graphs it takes ~800 seconds for Bang Bang and ~3000 seconds for Proportional.
5. Add delay:
In reality are are tons of delays because nothing is instantaneous, so we modeled the delay between the time the coffee reaches a given temperature and when the temperature sensor records the
temperature.
Proportional Control:
The impact of the sensor delay for proportional is that there are no temperature measurements for the first ~450 seconds and then there is a huge jump that then goes back down to a more stable (but still slightly fluctuating) temperature.
The impact of the sensor delay is that the graph is shifted to the right. This makes sense because bang bang is just "on or off" so the delay in sensing should not change the shape of the graph.
Other delays that we should consider in a thermodynamic system is the time it takes for the heater itself to heat up.

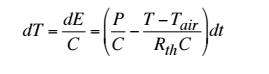













Great graphs and clear answers to the questions!
ReplyDeleteI really liked your analysis of the utility of bang-bang vs. proportional control for thermal systems.
ReplyDelete